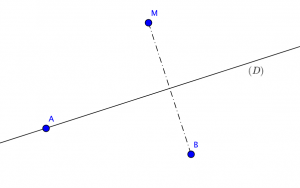
- Soient deux points $A$ et $B$ du plan. Soit $(D)$ une droite variable passant par $A$.
Soit $M$ le symétrique orthogonal de $B$ par rapport à $(D)$.
Que peut-on dire de $\Gamma$ le lieu de $M$ lorsque $(D)$ varie ?
Comme $A \in (D)$ alors la symétrie $S_{(D)}$ transforme $A$ en $A$.
Cette symétrie transforme $B$ en $A$.
Comme une symétrie orthogonale est une isométrie c'est-à-dire qu' il y a conservation des distances
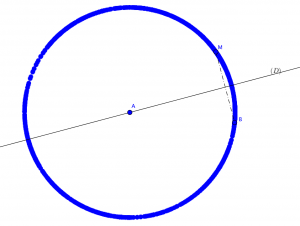
par conséquent, $AM = AB$ donc $M$ appartient au cercle de centre $A$ et de rayon $AB$.
Alors $\Gamma \subset \mathcal{C}(A ; AB)$
- Soit un cercle $\mathcal{C}(O ; R)$. Soit $A$ un point fixe situé à l'extérieur de $\mathcal{C}$.
Soit $P$ un point variant sur $\mathcal{C}$. La droite $(AP)$ recoupe le cercle $\mathcal{C}$ en $P'$. Soit $M$ le milieu du segment $[PP']$.
Que peut-on dire de $\Gamma$ le lieu de $M$ lorsque $P$ varie sur $\mathcal{C}$ ? - Soient $A$ et $B$ deux points distincts du plan.
Soit $\mathcal{C}$ le cercle de diamètre $[AB]$.
Soit $M$ un point de $\mathcal{C}$ distinct de $A$ et de $B$.
a) Quelle est la nature du triangle $AMB$ ?
b) Soit $N$ le symétrique de $A$ par rapport à $M$.
Quel est le lieu géométrique de $N$ lorsque $M$ varie sur $\mathcal{C}$ ?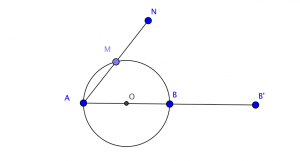
Comme $N$ est le symétrique de $A$ par rapport à $M$ alors $\overrightarrow{AN} = 2 \overrightarrow{AM}$ donc l'homothétie $H$ de centre $A$ et de rapport $2$ transforme $M$ en $N$
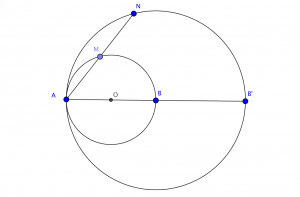
Or $M$ décrit le cercle de centre $O$ milieu de $[AB]$ et de rayon $\dfrac{AB}{2}$ donc $N$ va décrire l'image de ce cercle par l'homothétie $H$ à savoir un cercle de centre $H(O) = B$ et de rayon $2 \dfrac{AB}{2} = AB$.
Mais $M \neq A$ et $M \neq B$ donc comme $H(A) = A$ et $H(B) = B'$ alors le lieu de $N$ est le cercle $\mathcal{C}(B,AB)$ privé des points $A$ et $B'$.
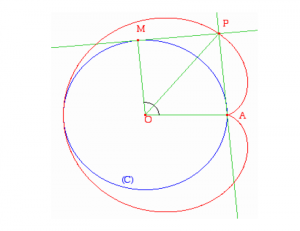
- Soit un cercle $(C)$ de centre $O$ passant par un point $A$. Soit $M$ un point de ce cercle. Soit $P$ le projeté orthogonal de $A$ sur la tangente en $M$ au cercle ; \\
Quel est le lieu du point $P$ lorsque $M$ décrit $(C)$ ?
Aller au contenu
