- Séries statistiques à 2 variables quantitatives
- Définition
Dans un échantillon de taille $n$ extrait d'une population donnée, on peut observer pour chaque individu 2 caractères $X$ et $Y$ qui prennent respectivement les valeurs $x_1,x_2,\cdots,x_n$ et $y_1,y_2,\cdots,y_n$.
L'ensemble des résultats ou observations concernant 2 caractères de cette population forme une série statistique à 2 variables ou une série statistique double. - Exemples
On peut avoir des séries statistiques concernant :
1 - La taille et le poids d'une population d'enfants
2 - Le nombre de pièces d'une série de logements et leur surface.
3 - Le nombre de chômeurs et le nombre de cotisations à recouvrer.
4 - L'effectif global d'une entreprise et le nombre d'agents suivant une formation.
5 - La production d'un service et le nombre d'heures supplémentaires.
6 - Le nombre de postes de radio et le nombre de maladies mentales.
- Variable explicative et variable expliquée
Une des variables s'appelle $X$ prend des valeurs $x_1,x_2,\cdots,x_p$. On l'appelle la variable explicative.
L'autre variable s'appelle $Y$ prend des valeurs $y_1,y_2,\cdots,y_p$. On l'appelle la variable expliquée.
On obtient ainsi un nuage de points de coordonnées $(x_i,y_i$ que l'on peut représenter dans un repère orthogonal d'axes $(Ox)$ et $(Oy)$.
- Définition
- Tableaux d'effectifs, fréquences marginales , fréquences conditionnelles
L'ensemble des $n$ résultats ou observations $(x_i,y_i)$ peut se présenter de $2$ façons :
- soit sous forme de $n$ données non groupées
Individu 1 2 ... i ... n X $x_1$ $x_2$ $x_i$ $x_n$ Y $y_1$ $y_2$ $y_i$ $y_y$
- soit sous forme de $n$ données groupées (ici $p = q = n)$
X Y
$y_1$ $y_2$ $\cdots$ $y_i$ $\cdots$ $y_n$ Totaux : effectifs marginaux en $x$ $x_1$ $n_{11 }$ $n_{12 }$ $n_{1i }$ $n_{1q }$ $n_{1.}$ $x_2$ $n_{21 }$ $n_{22 }$ $n_{ 2i}$ $n_{2q }$ $n_{2.}$ $\cdots$ $x_i$ $n_{i1 }$ $n_{ i2}$ $n_{ ii}$ $n_{iq }$ $n_{i.}$ $\cdots$ $x_p$ $n_{ p1}$ $n_{p2 }$ $n_{pi }$ $n_{pq}$ $n_{p.}$ Totaux : Effectifs marginaux en $y$ $n_{.1}$ $n_{.2}$ $n_{.i}$ $n_{.q}$ n - Soit la série statistique $\{(x_i;y_j;n_{ij})/ i =1..p,j =1..q \}$
- $n_{ij}$ est l'effectif du couple $(x_i;y_j)$ c'est-à-dire le nombre de couples $(X,Y)$ pour lesquels $X = x_i$ et $Y =y_j$
- $n_{i.} = \sum_{j=1}^q n_{ij}$ est l'effectif marginal de la valeur $x_i$ c'est-à-dire le nombre de couples $(X,Y)$ pour lesquels $X = x_i$
- $n_{.j} = \sum_{i=1}^p n_{ij}$ est l'effectif marginal de la valeur $y_j$ c'est-à-dire le nombre de couples $(X,Y)$ pour lesquels $Y = y_j$
- $n = \sum_{i=1}^p n_{i.} = \sum_{j = 1}^q n_{.j} = \sum_{i=1}^p \sum_{j = 1}^q n_{ij}$
- la série statistique $\{(x_i;n_{i.})/ i = 1..p \}$ s'appelle la distribution marginale de $X$
- la série statistique $\{(y_j;n_{.j})/ j = 1..q \}$ s'appelle la distribution marginale de Y
- $f_{ij} = \dfrac{n_{ij}}{n}$ est la fréquence du couple $(x_i:y_j)$
- $f_{i.}=\sum_{j=1}^q f_{ij}$ est la fréquence marginale de la valeur $x_i$ de $X$
- $f_{.j}=\sum_{i=1}^p f_{ij}$ est la fréquence marginale de la valeur $y_j$ de $Y$
-
- la série statistique $\{(x_i,n_{ij})/ i =1..p \}$ s'appelle la distribution conditionnelle de $X$ sachant que $Y$ vaut $y_j$
- la série statistique $\{(y_j,n_{ij})/ j =1..q\}$ s'appelle la distribution conditionnelle de $Y$ sachant que $X$ vaut $x_i$
- $\dfrac{n_{ij}}{n_{.j}}$ est la fréquence conditionnelle de la valeur $x_i$ sachant $y_j$
- $\dfrac{n_{ij}}{n_{i.}}$ est la fréquence conditionnelle de la valeur $y_j$ sachant $x_i$
- Soit la série statistique $\{(x_i;y_j;n_{ij})/ i =1..p,j =1..q \}$
- Valeurs caractéristiques
- Cas d'un nuage de points en forme de fuseau : ajustement affine par une droite de régression.
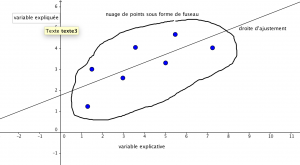
- Commentaires sur la méthode de régression linéaire :
La méthode de régression linéaire est un outil statistiques intéressant car :
- elle permet de synthétiser l'information numérique.
- elle fournit un modèle explicatif en mettant des évidences des liaisons
- elle constitue un outil de prévision
Si l'outil reste séduisant, c'est l'étude du coefficient de corrélation $r$ qui permet d'apprécier la valeur de la relation mise en évidence, sa fiabilité et de définir le champ de son utilisation ultérieure. - Commentaires sur le rôle du coefficient de corrélation :
- C'est un nombre $r$ qui est toujours compris entre -1 et 1.
- Si $r$ est proche de -1 ou de 1 la corrélation est satisfaisante et le modèle calculé est valable.
- On considère qu'un bonne corrélation est exprimée par un $-1 < r <-0,8$ ou $0,8 < r < 1$.
- Il faut être d'autant plus exigeant sur $r$ que le nombre d'observations est faible.
- si $r$ est proche de $0$ la corrélation est faible et donc la liaison entre les 2 phénomènes n'est pas de bonne qualité.
- Si $r > 0$ alors les phénomènes évoluent dans le même sens.
- Si $r < 0$ alors la liaison est inverse c'est-à-dire que les phénomènes évoluent en sens contraires
- Attention aux prévisions : il faut être prudent car les prévisions peuvent être soumises à des aléas qui peuvent modifier la droite prudemment calculée.
- Attention aux conclusions trop hâtives d'un bon $r$ :
Ne pas confondre corrélation et causalité : il est possible qu'il n'y ait aucun lien direct de cause à effet entre $X$ et $Y$.
Cette vision peut être toute relative. Il faut donc réfléchir aux mécanismes qui peuvent leur 2 variables étudiées.
Dans certains cas, $X$ et $Y$ peuvent dépendre toutes les deux d'une variable $Z$ : on parle alors de covariation. - Exemple de corrélation et de non-causalité
On considère les 2 chroniques suivantes où pour l'année $i$ , $x_i$ est le nombre de postes radio en service en France et $y_i$ est le nombre de maladies mentales déclarées pour 10000 habitants.
Année Nombre de poste radio Nombre de maladies mentales déclarées pour 10000 habitants 1928 2700 11 1929 3100 11 1930 3600 12 1931 4600 16 1932 5500 18 1933 6300 19 1934 7000 20 1935 7600 21 1936 8100 22 1937 8600 23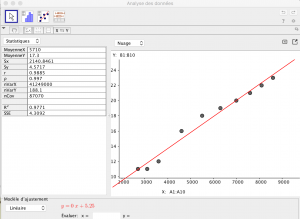 
Le nuage de points est en fuseau et après calculs (ici obtenus avec le logiciel Geogebra)
on trouve :
$\overline{x} = 5710$ ; $\overline{y} = 17,3$ ; $a =0,002$; $b = 5,247$ ; $r =0,988$.
Que pensez-vous de la valeur scientifique de l'affirmation suivante :" L'écoute de la radio altère la santé mentale des auditeurs "?
Cette affirmation est fausse car bien que la corrélation est très forte cela ne veut pas dire qu'il y a une causalité directe entre les deux variables.
- Commentaires sur la méthode de régression linéaire :
Aller au contenu
