Pour caractériser une série statistique en plus des paramètres de position il faut disposer de paramètres de dispersion
- L'étendue ou l'amplitude $Max -Min$ :
C'est la différence entre la plus grande valeur et la plus petite valeur observée.
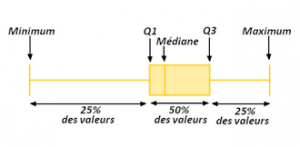
C'est une valeur facile à calculer mais comme elle ne tient compte que des valeurs extrêmes , elle risque d'être affectée par une valeur exceptionnelle ou une valeur erronée de ces observations. - L'intervalle interquartiles $Q_3 - Q_1$ :
Il est moins sensible que l'étendue aux valeurs extrêmes.
- Les $2$ paramètres précédents ont un handicap : ils ne nous renseignent pas sur la distribution des valeurs de la série statistique par rapport à la moyenne.
- L'écart-absolu moyen eam:
L'écart absolu moyen = $\dfrac{\sum_{i=1}^p n_i (x_i - \overline{x})}{\sum_{i=1}^p n_i }$
C'est la moyenne pondérée des écarts à la moyenne.
Il est peu employé dans les calculs statistiques car les valeurs absolues prêtent mal aux calculs algébriques. - L'écart-type $\sigma$ :
- L'écart-type est la racine carrée de la variance, la variance $V =\sigma^2$ étant la moyenne des carrés des écarts à la moyenne.
Les carrés des écarts à la moyenne par contre, se plient plus facilement aux calculs d'où l'intérêt de l'écart-type $\sigma$ qui est la racine carrée de la variance.
$V = \dfrac{\sum_{i=1}^p n_i(x_i - \overline{x})^2}{\sum_{i=1}^p n_i}$
Plus $\sigma$ est faible, plus les écarts à la moyenne le sont aussi et moins la série statistique est dispersée.
$\sigma$ est un indicateur de dispersion très fréquemment utilisé car il présente l'avantage d'être du même ordre de grandeur que la série observée. Ce qui n'est pas le cas de la variance.
Enfin son calcul est nécessaire pour déterminer la précision d'une estimation par la technique du sondage. - $\sigma$ obéit aussi à L'Inégalité de BienAimé-Tchebychev :
$\forall k > 0 \qquad P( [\overline{x} - k \sigma \leq X \leq \overline{x} + k \sigma]) \leq \dfrac{1}{k^2}$
Par exemple, pour $k = 2$
$ P( [\overline{x} - 2 \sigma \leq X \leq \overline{x} + 2\sigma]) \leq \dfrac{1}{4}$
Par exemple, pour $k = 3$
$ P( [\overline{x} - 3 \sigma \leq X \leq \overline{x} + 3\sigma]) \leq \dfrac{1}{9}$ - Cas particulier d'une série statistique suivant la loi normale de Laplace-Gauss
- L'écart-type est la racine carrée de la variance, la variance $V =\sigma^2$ étant la moyenne des carrés des écarts à la moyenne.
- Les coefficients de dispersion relative
- Le coefficient de variation $\dfrac{\sigma}{\overline{x}}\times 100$
Ce coefficient s'exprime en pourcentage. Il ne dépend pas des unités de mesure employées ou par leur nature.
Exemple 1 :
Dans une entreprise en 1975 le salaire annuel moyen des cadres et ingénieurs était de 70 500 F avec un écart-type de 17 000 F et la salaire horaire moyen des ouvriers était de 12,50 F avec un écart-type de 2,30 F.
Pour les cadres, $\dfrac{\sigma}{\overline{x}}\times 100 = \dfrac{17000}{70500}\times 100 = 24,11 \% $.
Pour les ouvriers, $\dfrac{\sigma}{\overline{x}}\times 100 = \dfrac{2,30}{12,50}\times 100 = 18,4 \% $.
Exemple 2 :
Dans un examen un correcteur 1 a donné une série de notes dont la moyenne est 8 et l'écart-type 4,25 et un correcteur 2 a donné une série de notes dont la moyenne est 10 et l'écart-type 4,5 .
Pour le correcteur 1, $\dfrac{\sigma}{\overline{x}}\times 100 = \dfrac{4,25}{8}\times 100 = 53 \% $.
Pour le correcteur 2 $\dfrac{\sigma}{\overline{x}}\times 100 = \dfrac{4,5}{10}\times 100 = 45 \% $.
Le correcteur 2 a des notes plus élevées (2 points de plus en moyenne) et ses notes sont plus concentrées autour de la moyenne que celles du correcteur 1. - Le coefficient inter-quartile relatif $\dfrac{Q_3 - Q_1}{Q_2}$
$Q_1$ est le premier quartile, $Q_2$ est le deuxième quartile ou encore la médiane $Me$, $Q_3$ est le 3ème quartile.
- Le coefficient de variation $\dfrac{\sigma}{\overline{x}}\times 100$

