-
- Résultats de base à connaître par coeur
- 8 identités remarquables dans l'ensemble des réels(mieux dans tout anneau commutatif) :
- $IR_1$ : $(a +b)^2 = a^2 + 2ab + b^2$
démonstration :
$(a +b)^2 =(a + b)(a + b) = a^2 +ab + ab + b^2 =a^2 + 2ab + b^2$
Le carré d'une somme est la somme du double produit et des carrés des deux nombres.
 Attention, le carré d'une somme n'est pas la somme des carrés d'autant plus que la fonction carré n'est pas une fonction linéaire !
Attention, le carré d'une somme n'est pas la somme des carrés d'autant plus que la fonction carré n'est pas une fonction linéaire !
Attention, il ne faut jamais oublier le double produit : vous pouvez le vérifier en observant bien le schéma suivant :

- $IR_3$ : $(a - b)^2 = a^2 - 2ab + b^2$
démonstration :
- soit on remplace $b$ par $-b$ dans l'identité remarquable $IR_1$
- soit on calcule : $(a -b)^2 =(a - b)(a - b) = a^2 -ab - ab + b^2 =a^2 - 2ab + b^2$
- vous pouvez le vérifier en observant bien le schéma suivant :

- $IR_3 $ :$(a + b)(a - b) =a^2 - b^2$
Démonstration :
- par le calcul : $(a + b)(a - b) = a^2 -ab + ba - b^2 = a^2 - b^2$
- vous pouvez le vérifier en observant bien le schéma suivant :

- $IR_4$ : $(a + b)^3 =a^3 + 3a^2 + 3ab^2 + b^3$
- $IR_5$ :$(a - b)^3 =a^3 - 3a^2 + 3ab^2 - b^3$
Il est assez facile de retenir ces identités remarquables en utilisant le triangle dit de PASCAL ou le triangle de SHU SHI YIE et la formule du binôme de Newton : - $IR_6$ : $\displaystyle{(a + b)^n = \sum_{k = 0}^n \binomial(n,k) a^k b^{n - k}}$

- $IR_7$ : $a^3 + b^3 = ( a + b)(a^2 -ab + b^2)$
- $IR_8$ : $a^3 - b^3 = ( a - b)(a^2 +ab + b^2$
- $IR_9$ : $(a + b + c)^2 =a^2 + b^2 + c^2 + 2ab + 2ac + 2bc$
- $IR_{10}$: Pour tout entier $n$ > 1,
$a^n - b^n = (a - b)(a^{n - 1} + a^{n - 2}b + \cdots + ab^{n - 2} + b^{n - 1})$- Exercice 1
Calculer mentalement $101^2$ ; $204^2$ ; $101 \times 99$ ; $394 \times 406$ ; $47^2 - 43^2$ - Exercice 2
Compléter les égalités suivantes :
$x^2 + \cdots + 25 = ( ...... + ......)^2$
$x^2 + \cdots + 16 = ( ...... + ......)^2$
$x^2 + \cdots + 16 a^2 = ( ...... + ......)^2$
$x^2 + \cdots + 16 a^2 = ( ...... - ......)^2$
$x^2 + 8x + \cdots = ( ...... + ......)^2$
$x^2 - 10 x + \cdots.= ( ...... - ......)^2$
$x^2 + 6x + \cdots = ( ...... + ......)^2$
$x^2 - 12 x +\cdots = ( ...... - ......)^2$
- Exercice 1
- Résultats de base à connaître par coeur
- Théorème du signe du binôme $ax +b$ avec $a \neq 0$
$x$ $-\infty$ $\frac{-b}{a}$ $+\infty$ $ax + b$ signe contraire de $a$ 0 signe de $a$
Ce théorème permet de résoudre aisément
-
- une équation du type $ax + b = 0$
- une inéquation du type $ax + b \geq 0$
- une inéquation-produit du type $(ax + b)(cx + d) \geq 0$
- une inéquation-quotient du type $\dfrac{ax + b}{cx +d} < 0$
- Théorème du signe du trinôme $ax^2 + bx + c$ avec $a \neq 0$
- 1er cas : le discriminant $\Delta < 0$
$x$ $-\infty$ $+\infty$ $ax^2 + bx + c$ signe de $a$
- 2ème cas : le discriminant $\Delta > 0$
$x$ $-\infty$ $\frac{-b}{2a}$ $+\infty$ $ax^2 + bx + c$ signe de $a$ 0 signe de $a$
- 3ème cas : le discriminant $\Delta > 0$
$x$ $-\infty$ $x'$ $x"$ $+\infty$ $ax^2 + bx + c$ signe de $a$ 0 signe contraire de $a$ 0 signe de $a$
Ce théorème sous forme de 3 tableaux permet de résoudre aisément - une équation du type $ax^2 + bx + c = 0$
- une inéquation du type $ax^2 + bx + c \geq 0$
- une inéquation-produit du type $(ax^2 + bx + c)(dx^2 + ex + f) \leq 0$
- une inéquation-quotient du type $\dfrac{ax^2 + bx + c}{dx^2 + ex + f} < 0$
- 1er cas : le discriminant $\Delta < 0$
- Comment résoudre une équation ou une inéquation d'inconnue $x$?
- 1ère étape : chercher l'ensemble de définition $Def$ de cette équation c'est-à-dire l'ensemble des $x$ pour lesquels les membres de cette équation (ou inéquation) existent.
- 2ème étape : Pour tout $x \in Def$ résoudre cette équation par équivalence logique.
- 3ème étape : Vérifier que les solutions trouvées appartient bien à l'ensemble de définition puis écrire l'ensemble des solutions $\mathcal{S}$
Exemple : Résoudre l'équation suivante $\dfrac{3x - 5}{x + 1} = \dfrac{-7}{x} + \dfrac{7 - x}{x^2 + x}$ d'inconnue $x \in R$- $Def =\{ x / x + 1 \neq 0 \text{ et } x \neq 0 \text{ et } x^2 + x \neq 0\}$
Comme $x + 1 = 0 \iff x = -1$
Comme $x^2 + x = 0 \iff x(x + 1) = 0 \iff x = 0 \text{ ou } x = -1$
alors $Def = R - \{ -1 ; 0\}$ - $\forall x \in Def$ on a $\dfrac{3x - 5}{x + 1} = \dfrac{-7}{x} + \dfrac{7 - x}{x^2 + x}
\iff \dfrac{x(3x - 5)}{x(x + 1)} = \dfrac{-7(x + 1)}{x(x + 1)} + \dfrac{7 - x}{x^2 + x}$
$\iff x(3x - 5) = -7(x + 1) + 7 - x \iff 3x^3 - 5 x = -7 x - 7 + 7 - x \iff 3x^2 -5x = -8x$
$\iff 3x^2 + 3x = 0 \iff 3x( x + 1) = \iff x =0 \text{ ou } x = -1$ - $0 \notin Def$ et $-1 \notin Def$ donc $\mathcal{S} = \emptyset$
- $Def =\{ x / x + 1 \neq 0 \text{ et } x \neq 0 \text{ et } x^2 + x \neq 0\}$
- Comment encadrer avec 13 règles de base ?

- $R_1$ : $a,m,m',M$ étant des nombres réels
Si $m \leq a \leq M$ alors $m + m' \leq a + m' \leq M + m'$
On peut ajouter ou retrancher aux 3 membres d'une double inégalité la même valeur - $R_2$ :

Attention , pour la multiplication de deux membres d'une inégalité par un même nombre, il faut s'inquiéter du signe de ce nombre.
$a,m,m',M$ étant des nombres réels- Si $m' > 0$, Si $m \leq a \leq M$ alors $m m' \leq a m' \leq M m'$ : l'ordre est conservé.
- Si $m' < 0$, Si $m \leq a \leq M$ alors $m m' \geq a m' \geq M m'$ : l'ordre est renservé.
Exemple classique : $ln(0.2) x \leq ln(8) \iff x \geq \dfrac{ln(3)}{ln(0,2)}$ car $ln(0,2) < 0$ puisque $0< ln(2) < 1$
- $R_3$ : $a,b, m,m',M,M'$ étant des nombres réels
Si $m \leq a \leq M$
Si $m' \leq b \leq M'$
alors $m + m' \leq a + b \leq M + M'$ - $R_4$ : $a,b, m,m',M,M'$ étant des nombres réels

Si $m \leq a \leq M$
Si $m' \leq b \leq M'$
alors $-m' \geq -b \geq -M'$
donc $m \leq a \leq M$
$-M' \leq - b \leq -m'$
Par conséquent, $m -M' \leq a - b \leq M -m'$ - $R_5$ : $a,b, m,m',M,M'$ étant des nombres réels
Si $0 \leq m \leq a \leq M$
Si $0 \leq m' \leq b \leq M'$
alors $m + m' \leq a b \leq M + M'$ - $R_6$ :
- $R_7$ :
- $R_8$ :
- $R_9$ :
- $R_{10}$ :
- $R_{11}$ :
- $R_{12}$ :
- $R_{13}$ :
- $R_1$ : $a,m,m',M$ étant des nombres réels
- Aider l'élève à maîtriser les expressions algébriques :
- Maîtriser la notion de valeur absolue d'un nombre réel :
 Retenons :
Retenons :
La valeur absolue d'un nombre est sa distance à $0$ : $\mid x \mid = d(x ; 0)$Pour déterminer la valeur absolue d'un nombre x, on utilise un algorithme :On détermine d'abord le signe de ce nombreSi ce signe est positif alors la valeur absolue de ce nombre est ce nombre.Si ce signe est négatif alors la valeur absolue de ce nombre est l'opposé de ce nombre.
Exercice 1
Déterminer les valeurs absolues des nombres suivants :56 ; - 75 ; 3.14 ; $x^2$ ; $-x^4$
Retenons :
Voici la courbe d'équation y =| x | Application aux équations
Application aux équations
Retenons : 1°) Si $a < 0$ alors l'équation $|x| = a$ n'a aucune solution car la valeur absolue d'un nombre est toujours positive ou nulle2°) Si $a > 0$ alors l'équation $|x| = a$ admet pour solutions $-a$ et $a$ car deux nombres opposés ont même valeur absolue 3°) Si $a = 0$ alors l'équation $|x| = a$ admet pour solution unique $0$ car la valeur absolue d'un nombre est nulle si et seulement si ce nombre est nul.Exercice Résoudre les équations suivantes d'inconnue x :a) $|x| = -3$
1°) Si $a < 0$ alors l'équation $|x| = a$ n'a aucune solution car la valeur absolue d'un nombre est toujours positive ou nulle2°) Si $a > 0$ alors l'équation $|x| = a$ admet pour solutions $-a$ et $a$ car deux nombres opposés ont même valeur absolue 3°) Si $a = 0$ alors l'équation $|x| = a$ admet pour solution unique $0$ car la valeur absolue d'un nombre est nulle si et seulement si ce nombre est nul.Exercice Résoudre les équations suivantes d'inconnue x :a) $|x| = -3$
b) $|x| = 7$
c) $|x - 3| = -3$
d) $|x - 3| = 0$
Retenons :
La distance entre des nombres $a$ et $b$ est la valeur absolue de leur différence.
On écrira $d(a;b) = | a - b |$
Exercice
1°)Calculer $d(3;4) ; d( 4;-7) ; d(-7;-11)$2°) Résoudre en utilisant la notion de distance l'équation : $|x - 3| = 2$
Retenons :
1°)Si $a <= 0$ alors $|nombre|< a$ est impossible
2°)Si $a > 0$ alors $|nombre| < a$ signifie que ce nombre est strictement compris entre $- a$ et $a$

3°)Si $a < 0$ alors $|nombre|> a$ est vraie pour tout nombre.
4°)Si $a >= 0$ alors $|nombre| > a$ signifie que ce nombre est strictement plus petit que $-a$ ou strictement plus grand que $a$.


- Maîtriser la notion de partie entière d'un nombre réel :
Retenons :
Tout nombre réel $x$ est compris entre 2 entiers relatifs consécutifs $n$ et $n + 1$.
On a donc $\forall x \ in R \qquad n \leq x < n + 1$
Cet entier relatif $n$ s'appelle la partie entière de $x$ et se note $[x]$.
La partie entière d'un réel est donc le plus grand de tous les entiers relatifs qui le précèdent.
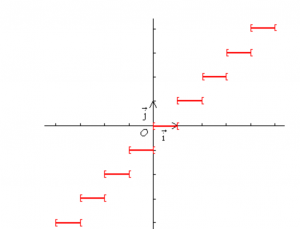 Comme $[x] \leq x < [x] +1$ alors $0 \leq x - [x] < 1$.
Comme $[x] \leq x < [x] +1$ alors $0 \leq x - [x] < 1$.
$x \mapsto x - [x]$ s'appelle la fonction partie fractionnaire de $x$. C'est une fonction périodique de période $1$
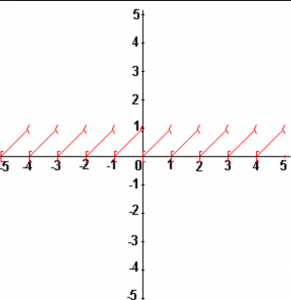
Entrainement :
Sujet sur la partie entière : partieentiere
Corrigé : partieentierecor

