Définition d'une homothétie de centre $O$ et de rapport $k \neq 0$:
Soit $E$ un espace affine de dimension $n$.
Si $n = 2$ alors $E$ est un plan.
Si $n = 3$ alors $E$ est l'espace.
Soit un réel $k \neq 0$. Soit un point $O$ de $E$.
On appelle Homothétie de centre $O$ et de rapport $k$ l'application de $E$ dans $E$ qui à tout point $A$ associe le point $A'$ tel que $\overrightarrow{O A'} = k \ \overrightarrow{OA}$.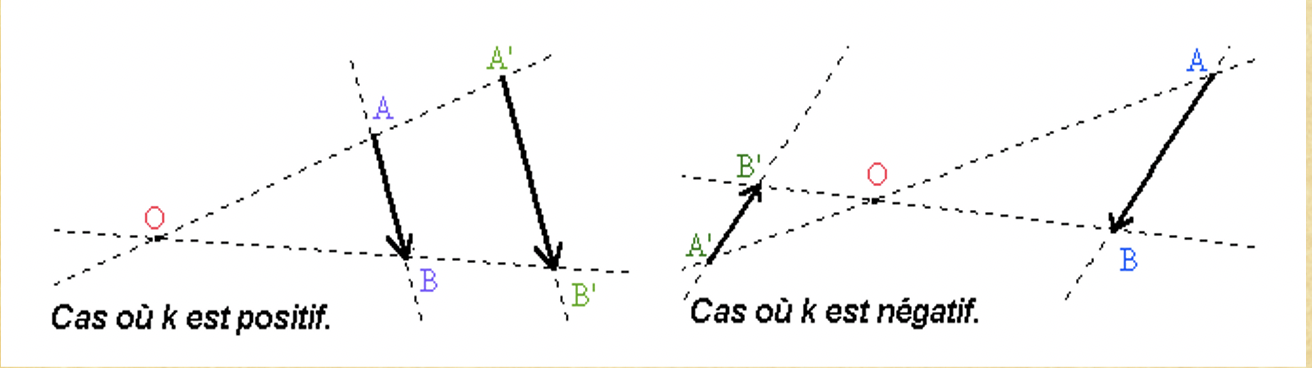
L'homothétie c'est en fait de l'agrandissement-réduction :
- L'homothétie fait de l'agrandissement lorsque $k < -1 \text{ ou } k >1$.
- L'Homothétie fait de la réduction lorsque $-1 < k < 1$
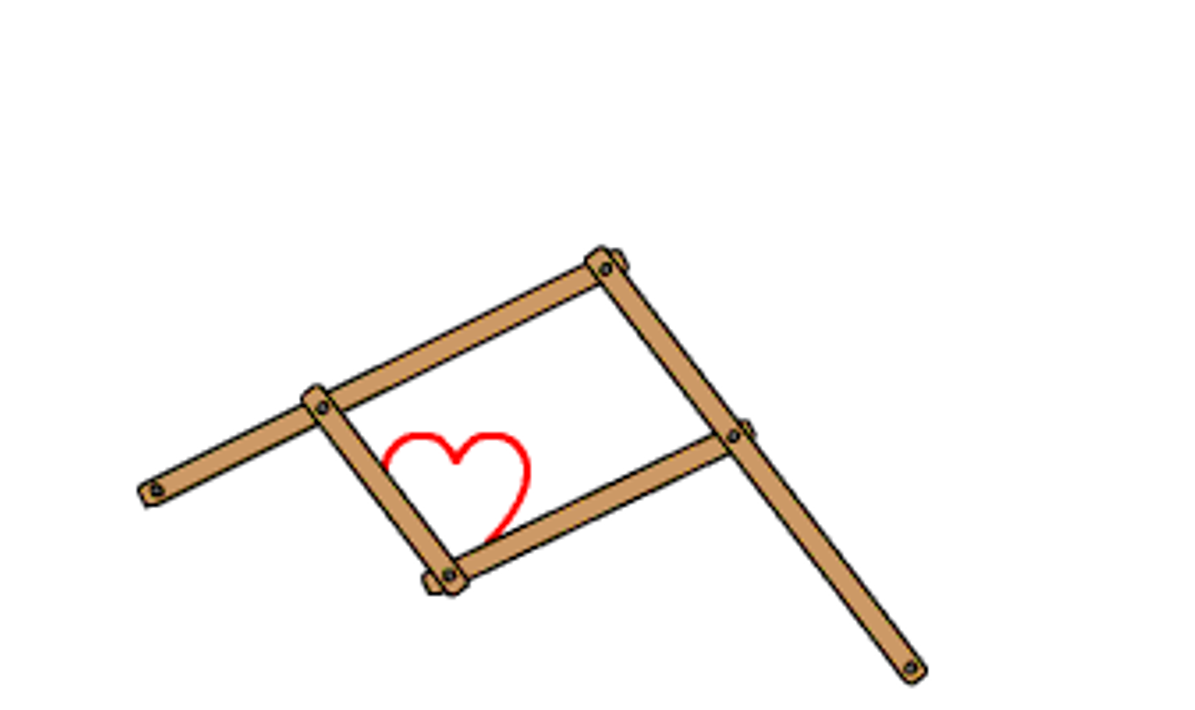
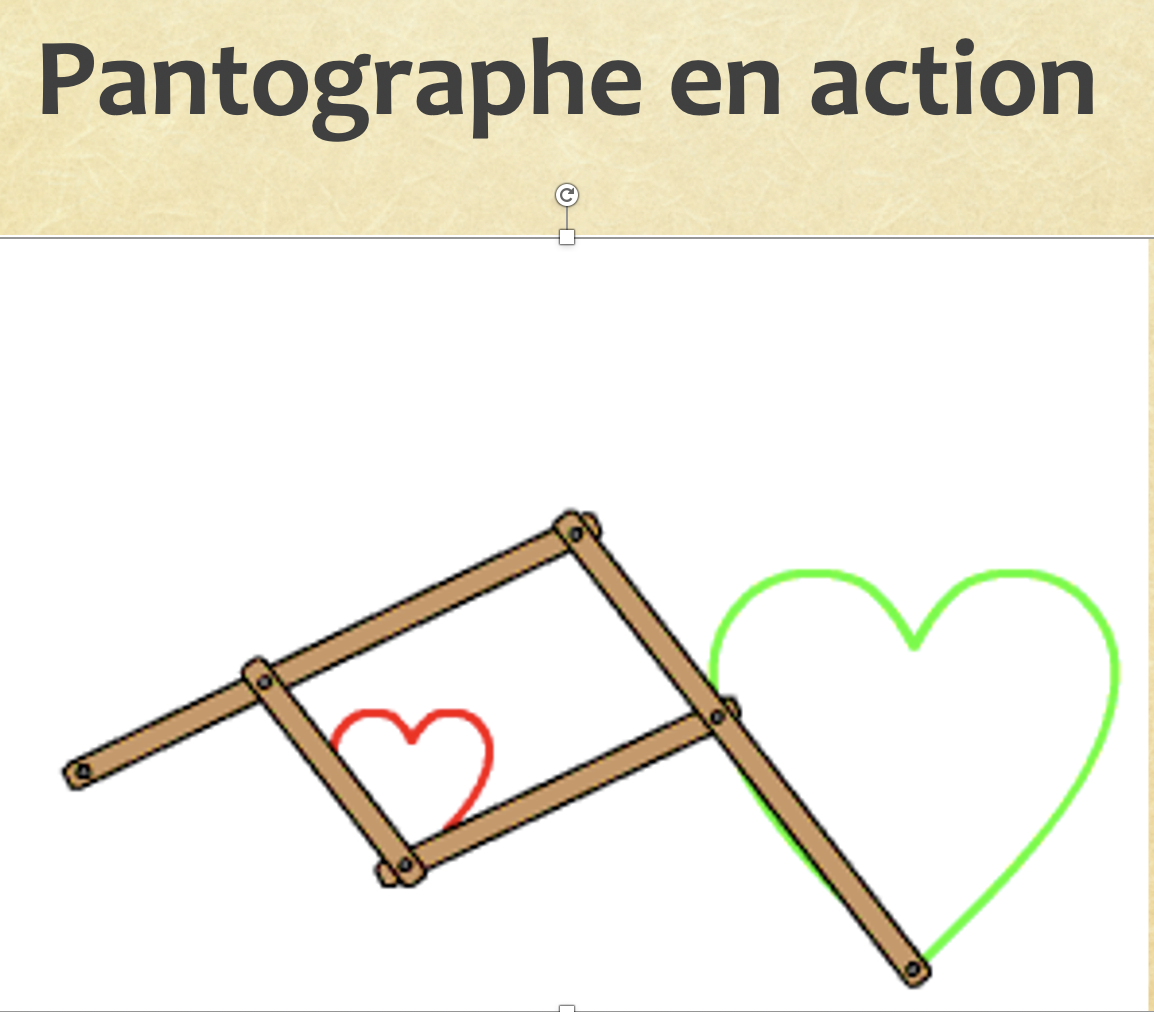
- L'appareil qui illustre elle mieux l'homothétie est le pantographe des graveurs :
Voici une image d'un pantographe professionnel :

Ce pantographe est celui utilisé par le célèbre graveur de Fort de France

Mr BOISSON
Propriétés d'une homothétie
Une homothétie est donc une application affine dont l'endomorphisme associé est l'homothétie vectorielle $h_k$ de rapport $k : $ qui est encore $k Id_{\overrightarrow{E}}$.
De plus, une homothétie étant bijective alors toute homothétie a toutes les propriétés d'une bijection affine.
Par conséquent, une homothétie transforme :
- le milieu $I$ du bipoint $(A,B)$ en le milieu $I'$ du bipoint $(A',B')$
- une droite $(AB)$ en une droite $(A'B')$ parallèle.
- deux droites $(D_1)$ et $(D_2)$ parallèles en deux droites $(D'_1)$ et $(D'_2)$ parallèles.
- deux droites $(D_1)$ et $(D_2)$ perpendiculaires en deux droites $(D'_1)$ et $(D'_2)$ perpendiculaires.
- un angle géométrique $\widehat{ABC}$ en un angle géométrique $\widehat{A'B'C'}$ de même mesure.
- un cercle $\mathcal{C}(O;R)$ en un cercle $\mathcal{C}(O'; |k| \ R)$ avec $O' = H(O)$
- un domaine plan $\mathcal{D}$ d'aire $\mathcal{A}$ en un domaine $\mathcal{D'}$ d' aire $k^2 \ \mathcal{A}$.
- dans l'espace, une sphère $\mathcal{S}(O;R)$ en une sphère $\mathcal{S}(O';|k| \ R)$ avec $O' = H(O)$
- Action sur les longueurs, aires et volumes
- Attention, une homothétie n'est pas une isométrie à part $H(\Omega,1)$ et $H(\Omega,-1)$
- Par conséquent, une homothétie transforme :
- un cercle $\mathcal{C}(\Omega;R)$ en un cercle $\mathcal{C}(\Omega'; |k| \ R)$ avec $\Omega' = H(\Omega)$.
- un domaine $\mathcal{D}$ d'aire $\mathcal{A}$ en un domaine $\mathcal{D'}$ d' aire $k^2 \ \mathcal{A}$.
- dans l'espace, une sphère $\mathcal{S}(\Omega;R)$ en une sphère $\mathcal{S}(\Omega';|k| \ R)$ avec $\Omega' = H(\Omega)$.
- dans l'espace, un solide $V$ de volume $\mathcal{V}$ en un solide $V'$ de volume $|k|^3 \ \mathcal{V}$.
Cours personnel sur le groupe des homothéties-translations :

