 (photo : collection personnelle Laurent VALERE)
(photo : collection personnelle Laurent VALERE)
Le citoyen lambda qui passe devant le mémorial du Cap 110 ne voit qu'un groupe de statues face à la mer. S'il a la curiosité de lire les panneaux, il comprendra que cette oeuvre d'art s'érige là en la mémoire de disparus.
 Photo (Droits réservés)
Photo (Droits réservés)
L'individu curieux et un tant soit peu sensibilisé aux Mathématiques y voit une disposition géométrique particulière des statues.
Le professeur de Mathématiques lui, au delà de cette disposition géométrique, voit matière à faire découvrir aux élèves les nombres triangulaires.
La rencontre avec l'artiste Laurent VALERE, créateur de l'oeuvre, avec Le Sénateur ex-Maire du Diamant Mr Serge LARCHER le commanditaire de l'oeuvre et l'historienne Elisabeth LANDI nous a encouragé à jeter un regard mathématique sur cette oeuvre de L'anse Cafard.

Et si le créateur des statues avait continué : 6 statues au rang 6, 7 statues au rang 7, ..., n statues au rang n, combien y aurait-il en tout de statues, autrement dit que vaut la somme qu'on appelle le nombre triangulaire $T_n$
$ T_n = 1 + 2 + 3 + \cdots + (n \ - 1) + n $
Serez-vous capable de déterminer cette somme $T_n$ en utilisant 3 méthodes différentes ?
Méthode 1 (niveau CM2) : celle dite du Petit GAUSS du nom du génial mathématicien allemand Carl Friedrich GAUSS
On pose $ S = 1 + 2 + 3 + \cdots + n$
1°) Réécrire cette même somme dans l'autre sens
$ S = 1 + 2 + 3 + \cdots + n$
2°) Calculer alors $ 2S $
3°) En déduire que $ S = \dfrac{n( n + 1)}{2} $
Corrigé :
$S = \qquad 1 + \qquad 2 \ \ + \qquad 3 \ \ + \cdots + \qquad (n - 2) + (n - 1) + \qquad n$
$S = \qquad n + \ \ \ (n - 1) + \ \ ( n - 2) + \cdots + \qquad 3 \ \ \ + \qquad 2 \ \ \ + \qquad 1$
Par conséquent,
$2S = (n + 1) + (n + 1) + ( n + 1) + \cdots + (n + 1) + (n + 1) + (n + 1)$
Donc $2S = n(n + 1)$ d'où $S = \dfrac{n(n + 1)}{2}$
Méthode 2 (Chou pou têt) - niveau CM2
 Le nombre de jetons rouges est égal au nombre de jetons verts.
Le nombre de jetons rouges est égal au nombre de jetons verts.
Il y a 5 rangées de 6 jetons. Le nombre total de jetons est égal à 30 (soit $ 5 \times 6 $)
Le nombre de jetons rouge est donc 15 soit $ \dfrac{5 \times 6}{2} $
En généralisant à $ n $ rangées de $n + 1 $ jetons , le nombre total de jetons est $ \dfrac{n( n + 1)}{2} $
Méthode 3 - Par récurrence (niveau Terminale)
Notons $pr(n)$ la propriété suivante $1 + 2 + 3 + \cdots + (n - 1) + n = \dfrac{n(n + 1)}{2}$
Etape 1 . Initialisation
a -t-on $pr(1)$ ? c'est-à-dire a -t-on $1 = \dfrac{1(1 + 1)}{2}$?
Oui. Donc $pr(1)$ est vraie
Etape 2: Hérédité
Supposons que pour un certain entier naturel $n \geq 1$ la propriété $pr(n)$ est vraie donc supposons que $1 + 2 + 3 + \cdots + (n - 1) + n = \dfrac{n(n + 1)}{2}$
Alors $1 + 2 + 3 + \cdots + (n - 1) + n + ( n + 1) = \dfrac{n(n + 1)}{2} + n + 1 = \dfrac{n(n + 1) + 2(n + 1)}{2} = \dfrac{(n + 1)(n + 2)}{2} $ donc $pr(n + 1)$ est vraie
Conclusion
La propriété $pr$ est initialisée en $n = 1$ et est héréditaire donc est vraie pour tout entier naturel $n \geq 1$.
Méthode 4 - Niveau Première - Utilisation des polynômes $P(x)$ de degré $2$ tels que
$\forall x \in R \quad P(x + 1) - P(x) = x$
a) Déterminer un polynôme $P(x)$ de degré $2$ tel que $\forall x \in R \quad P(x + 1) - P(x) = x$
b) En déduire la valeur de $S_n = 1 + 2 + 3 + \cdots + n$
Démonstration
$\forall x \in R \quad P(x + 1) - P(x) = x \ iff a(x + 1)^2 + b(x + 1) + c = ax^2 + bx + c$
$\iff ax^2 + 2ax + a + bx + b + c = ax^2 + 2ax + c \iff 2ax + a + b = x \iff 2a = 1 \text{ et } a + b = 0$
(par identification des coefficients des monômes de même degré)
$\iff a = \dfrac{1}{2} \text{ et } b = \dfrac{-1}{2}$
L'ensemble des polynômes cherchés est donc l'ensemble des polynômes de la forme
$P(x) = \dfrac{1}{2} x^2 - \dfrac{1}{2} x + c$ où $c \in R$
Choisissons donc un de ces polynômes par exemple $P(x) = \dfrac{1}{2} x^2 - \dfrac{1}{2} x$
Comme $P(x + 1) - P(x) = x$ pour tout réel $x$ alors cette propriété est vraie pour tous les entiers naturels $1, 2, 3, \cdots n$
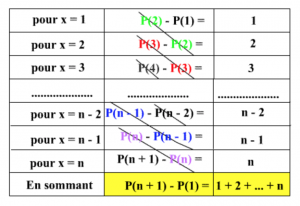 On obtient donc $P(n + 1) - P(1) = S$. or $P(1) = 0$
On obtient donc $P(n + 1) - P(1) = S$. or $P(1) = 0$
donc $S_n = P(n + 1) = \dfrac{1}{2} (n + 1)^2 - \dfrac{1}{2} (n + 1) = \dfrac{1}{2} (n + 1)[ n + 1 - 1]$
Par conséquent $S_n = \dfrac{n(n + 1)}{2}$
- Pour Aller plus loin :
Les nombres triangulaires se retrouvent très tôt dans les premiers travaux connus d'arithmétique portant sur les nombres figurés :- Les nombres triangulaires
- $T_1 = 1 $
- $T_2 = 1 + 2$
- $T_3 = 1+ 2 + 3$
- $T_4 = 1 + 2 +3 + 4 = 10 $ la célèbre Tentrakys adoré par les Pythagoriciens :
- $T_5 = 1 + 2 +3 + 4 + 5 = 15$ illustrée par le Cap 110.
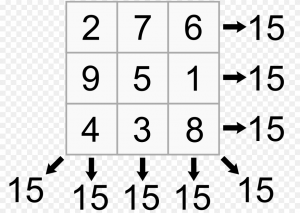
C'est aussi la somme magique intervenant dans les carrés magiques d'ordre $3$.
- Les nombres carrés
$1^2 \ ; \ 2^2 \ ; \ 3^2 \ ; \ \cdots$ - Les nombres pyramidaux
obtenus par empilement de carrés décroissants
$1^2 \ ; \ 1^2 + 2^2 \ ; \ 1^2 + 2^2 + 3^2 \ ; \ 1^2 + 2^2 + 3^2 + 4^2 \ ; \ \cdots$ - Les nombres tétraédriques
obtenus par empilement de nombres triangulaires consécutifs décroissants - Les nombres cubes
$1^2 \ ; \ 2^2 \ ; \ 3^2 \ ; \ \cdots$ - Les entiers naturels ainsi que les nombres triangulaires et tétraédriques se retrouvent dans les colonnes $3$ et $4$
du triangle de SHU CHI YE (1328) extrait du Miroir de jade des quatre éléments:
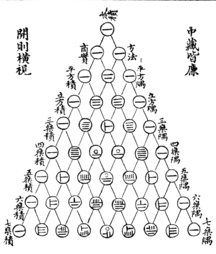 On retrouve des manuscrits plus anciens contenant ce tableau :
On retrouve des manuscrits plus anciens contenant ce tableau :
en Chine : Jia Xian(9ème siècle) ; Yang Qui (1261)
en Inde : BASKHARA II (1114-1185)
en Perse : al-Karaji(953-1029) ; Omar Khayyam(11è siècle) ;
au Maghreb : Ibn al Banna .
Ce tableau est plus communément appelé aussi triangle de Blaise PASCAL qui l'a exploité au maximum en particulier lorsqu'il crée la théorie des probabilités :

Ce triangle permet d'illustrer la formule dite du binôme de Newton(1642-1727) :
$\displaystyle{(a + b)^n = \sum_{k = 1}^n \ C_n^k \ a^k \ b^{n - k}}$ .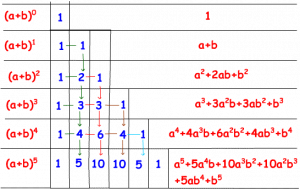
- Les nombres triangulaires
Cette formule était déjà connue au 10ème siècle en particulier par Ibn al Banna au Maghreb, Halayuda en Inde, Al Karaji en Perse et Yang Hui en Chine. Ce dernier la démontra.
- Exercice 1
Démontrer que pour tout entier naturel $n \geq 1$ on a :
$T_n =1^2 + 2^2 + 3^2 + \cdots + n^2 = \dfrac{n( n + 1)(2n + 1)}{6}$
a) par récurrence
b) en déterminant un polynôme $P(x)$ de degré $3$ tel que $\forall x \in R \quad P(x + 1) - P(x) = x^2$
Exercice 2
Démontrer par récurrence que $\forall n \in N^* \qquad U_n = 1^3 + 2^3 + \cdots /+n^3 = \F{n(n + 1)}{2})^2 = S_n^2$
Exercice 3
Retrouver les 4 sommes précédentes $S_n,T_n,U_n$ en utilisant des identités remarquables.
Exercice 4 (Rallye Math 2009 Lorraine)
Sylvain et Sylvette ont tous deux le même nombre de pièces de 1 centime. Ce nombre est strictement supérieur à 1.
Sylvain s'est amusé à les disposer en carré alors que Sylvette a préféré construire un triangle comme sur le modèle ci-dessus :
 A la fin de leur construction, il ne reste plus de pièces ni à l'un ni à l'autre.
A la fin de leur construction, il ne reste plus de pièces ni à l'un ni à l'autre.
Combien avaient-ils de pièces chacun, sachant de plus, que ce nombre de pièces est le plus petit nombre qui permette cette double construction? Justifier.
Exercice 6 (extrait Rallye FFJM)
 Jules, caissier dans un supemarché s'amuse tous les soirs à disposer en triangle le plus grand nombre possibles de pièces de 1 € de sa recette :
Jules, caissier dans un supemarché s'amuse tous les soirs à disposer en triangle le plus grand nombre possibles de pièces de 1 € de sa recette :
 Les pièces éventuellement en excès sont laissées de côté. Ensuite, il cherche à obtenir un triangle identique au premier triangle, mais avec la tête en bas, en déplacant le moins de pièces possible.
Les pièces éventuellement en excès sont laissées de côté. Ensuite, il cherche à obtenir un triangle identique au premier triangle, mais avec la tête en bas, en déplacant le moins de pièces possible.
 Hier soir, Jules a dû déplacer entre 99 et 109 pièces pour retourner son triangle.
Hier soir, Jules a dû déplacer entre 99 et 109 pièces pour retourner son triangle.
Il a utilisé toutes les pièces de sa recette et a trouvé la solution minimale du problème.
Quel était le montant en € de la recette de Jules ?

