
- Définition d'un cercle
Dans un plan affine euclidien , soit un réel $R \geq 0$ et un point $O$.
On appelle cercle de centre $O$ et de rayon $R$ l'ensemble des points $M$ tels que $OM = R$ - Angles inscrits et angle au centre
- Corollaire : Cercle et angle droit
Soit un cercle $\mathcal{C}$ de diamètre $[AB]$.
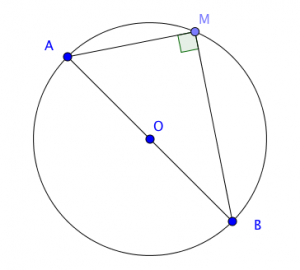
- Si $M \in \mathcal{C}$ alors le triangle $MAB$ est rectangle en $M$.
on dit encore que tout triangle inscriptible dans un demi-cercle est rectangle.
- Si le triangle $MAB$ est rectangle en $M$ alors $M \in \mathcal{C}$. - Autre Propriété caractéristique d'un cercle utilisant un diamètre $[AB]$
$M \in \mathcal{C}([AB]) \iff \overrightarrow{MA}.\overrightarrow{MB }= 0$ - Equation cartésienne d'un cercle dans un repère orthonormé
- Méthode 1 : $M(x;y) \in \mathcal{C}(\Omega ; R) \iff OM = R \iff OM^2 = R^2 \iff (x - x_{\Omega})^2 + (y - y_{\Omega})^2 = R^2$
- Méthode 2 : $M(x;y) \in \mathcal{C}([AB]) \iff \overrightarrow{MA}.\overrightarrow{MB }= 0$
$\iff (x_A - x)(x_B - x) + (y_A - y)(y_B - y) = 0$
$\iff x^2 + y^2 -x(x_A + x_B) - y(y_A + y_B) +x_A x_B +y_A y_B = 0$
- Problème réciproque : Qu'est ce que l'ensemble $\Gamma$ des points $M$ vérifiant une équation cartésienne du type $x^2 + y^2 + ax + by + c = 0$ dans un repère orthonormé ?
$M(x;y) \in \Gamma \iff x^2 + y^2 + ax + by + c = 0$
$\iff (x \ - \dfrac{a}{2})^2 + (y \ - \dfrac{b}{2})^2 = c \ - \dfrac{a^2}{4} \ - \dfrac{b^2}{4} $- ou bien $ c \ - \dfrac{a^2}{4} \ - \dfrac{b^2}{4}< 0$ alors $\Gamma =\emptyset$- ou bien $ c \ - \dfrac{a^2}{4} \ - \dfrac{b^2}{4}= 0$ alors $\Gamma =\{\Omega(\dfrac{a}{2} ; \dfrac{b}{2})\}$ = le cercle-point $\Omega$- ou bien $ c \ - \dfrac{a^2}{4} \ - \dfrac{b^2}{4}> 0$
alors $\Gamma =$ le cercle $\mathcal{C}$ de centre $\Omega(\dfrac{a}{2} ; \dfrac{b}{2})$ et de rayon $ \sqrt{c \ - \dfrac{a^2}{4} \ - \dfrac{b^2}{4}}$ - Systèmes d'équations paramétriques d'un cercle
- Cercle capable ou Cercle d'APPOLONIUS associé à deux points $A,B$ et un angle $\theta$
- Cercle d'Euler

Aller au contenu

