- Dnb 2018
- Pondichery
Sujet : Approximation de $\pi$ par la Méthode de Monte-Carlo
On lance une fléchette sur une plaque carrée sur laquelle figure une cible circulaire .
Si la pointe de la fléchette est sur le bord de la cible, on considère que la cible n'est pas atteinte.
On considère que cette expérience est aléatoire et l'on s'intèresse à la probabilité que la fléchette atteigne la cible.
- La longueur du côté de la plaque carrée est 200.
- Le rayon de la cible est 100.
- La fléchette est représentée par le point F de coordonnées $(x~;~y)$ où $x$ et $y$ sont des nombres
aléatoires compris entre $-100$ et $100$.
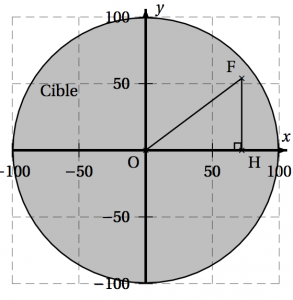On réalise un programme qui simule plusieurs fois le lancer de cette fléchette sur la plaque carrée et qui compte le nombre de lancers atteignant la cible. Le programmeur a créé trois variables nommées carré de OF, distance et score.
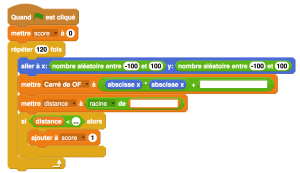1°) Lorsqu'on exécute ce programme, combien de lancers sont simulés ?2°) Quel est le rôle de la variable score ?3°) Compléter ce programme afin qu'il fonctionne correctement.4°) Après une exécution du programme, la variable score est égale à $102$.A quelle fréquence la cible a-t-elle été atteinte dans cette simulation ?Exprimer le résultat sous la forme d'une fraction irréductible.5°) On admet que la probabilité d'atteindre la cible est égale au quotient :
aire de la cible divisée par aire de la plaque carrée.6°) Quelle est la limite de cette fréquence lorsque le nombre de lancers devient très grand ?
En déduire une approximation de $\pi$.Corrigé
1°) Lorsqu'on exécute ce programme, $120$ lancers sont simulés.2°) La variable score à la fin du programme contient le nombre de fois où la fléchette a atteint la cible.3°)On compléte ce programme afin qu'il fonctionne correctement.
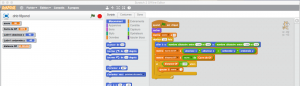4°) Si après une exécution du programme, la variable score est égale à $102$.Alors la fréquence à laquelle la cible a été atteinte est $f =\frac{102}{120} \approx 0,85$5°) La probabilité $p$ d'atteindre la cible est
$p = \dfrac{\pi \times Rayon^2}{cote^2} = \dfrac{\pi \times 100 \times 100}{200 \times 200} = \dfrac{\pi}{4} \approx 0,785$.6°) La limite de cette fréquence lorsque le nombre de lancers devient très grand est donc $\dfrac{\pi}{4}$.
De la simulation avec $1 000 000 $ lancers, on en déduit une approximation de $\pi$.
$\dfrac{\pi}{4} = \dfrac{777113}{1000000} \approx 0,777113$ donc $\pi \approx 3,108452$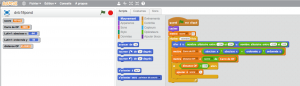
- Amérique du Nord
Sujet
Simon travaille sur un programme. Voici des copies de son écran :
Il obtient le dessin ci-dessous :
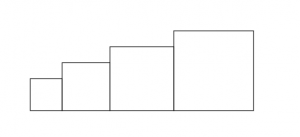1°) a) D'après le script principal, quelle est la longueur du côté du plus petit carré dessiné ?b) D'après le script principal, quelle est la longueur du côté du plus grand carré dessiné ?
2°) Dans le script principal, où peut-on insérer l'instruction
de façon à obtenir le dessin ci-contre ?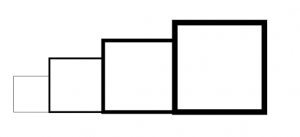
3°) On modifie maintenant le script principal pour obtenir celui qui est présenté ci-dessous :
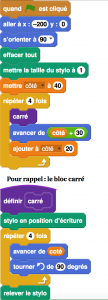Parmi les dessins ci-dessous, lequel obtient-on ?
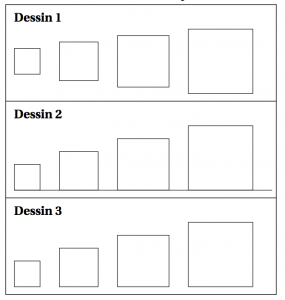Corrigé :1°) a) D'après le script principal, la longueur du côté du plus petit carré dessiné est $40$ car à l'entrée de la boucle la valeur de la variable côté est : $40$b) D'après le script principal, la longueur du côté du plus grand carré dessiné est $100$
En effet,
- Au premier tour de boucle, la variable côté contient $40$ , le carré est dessiné et à la fin de
ce tour on ajoute $20$ à la variable côté.
- Au deuxième tour, la variable côté contient $60$ , le deuxième carré est dessiné et à la fin de ce
tour on ajoute $20$ à la variable côté.
- Au troisième tour,la variable côté contient $80$ , le troisième carré est dessiné et à la fin de ce
tour on ajoute $20$ àla variable côté.
- Enfin, au dernier tour la variable côté contient $100$, le quatrième carré est dessiné.2°) Dans le script principal, on insére l'instruction
après l'instruction ajouter à côté $20$ de façon à obtenir le dessin ci-contre :
3°)Après la modification du script principal, le dessin obtenu est le dessin $3$.
En effet,
- Au premier tour de boucle, la variable côté contient $40$ , le carré est dessiné et à la fin de
ce tour on ajoute $20$ à la variable côté. Le stylo est alors relevé et on avance de $40 + 30$.
- Au deuxième tour, la variable côté contient $60$ , le deuxième carré est dessiné et à la fin de ce
tour on ajoute $20$ à la variable côté. Le stylo est alors relevé et on avance de $60 + 30$
- Au troisième tour,la variable côté contient $80$ , le troisième carré est dessiné et à la fin de ce
tour on ajoute $20$ àla variable côté. Le stylo est alors relevé et on avance de $80 + 30$
- Enfin, au dernier tour la variable côté contient $100$, le quatrième carré est dessiné.
- Pondichery
- Dnb 2017
Aller au contenu
