Formulaires

  • 12 Règles de calcul sur les quotients de nombres réels

    • Règle 1 : existence d'un quotient
      Un quotient de nombres réels existe si et seulement si son dénominateur est non nul
      Le quotient $ \dfrac{N}{D} = N \times \dfrac{1}{D}$ existe $\iff N$ existe et $D$ existe et $D \neq 0$
    • Règle 2 :
      $ N = \dfrac{N}{1}$
    • Règle 3 :
      si $D \neq 0$ alors $\dfrac{D}{D} = 1$
    • Règle 4 :
      $\dfrac{N}{D} = 1 \iff N = D $ lorsque $D \neq 0$
      $\dfrac{N}{D} < 1 \iff N < D $ lorsque $D>0$
      $\dfrac{N}{D} > 1 \iff N > D $ lorsque $D >0$
    • Règle 5 :
      si $D \neq 0$ alors
      $\dfrac{-N}{D} = \dfrac{N}{-D} = -\dfrac{N}{D}$
    • Règle 7 : Simplification d'une fraction
      si $D \neq 0$ et $k \neq 0$ alors
      $\dfrac{kN}{kD} = \dfrac{N}{D}$
    • Règle 8 : Somme de fractions ayant le même dénominateur
      si $D  \neq 0$  alors $\dfrac{N_1}{D} + \dfrac{N_2}{D} =  \dfrac{N_1 + N_2}{D}$
    • Règle 9 :
      si $D_1 \neq 0$ et  $D_2 \neq 0$ alors
      $\dfrac{N_1}{D_1} + \dfrac{N_2}{D_2} = \dfrac{N_1 D_2}{D_1D_2} + \dfrac{N_2D_1}{D_1D_2} = \dfrac{N_1D_2 + N_2D_1}{D_1D_2}$
    • Règle 10 :
      si $N_2 \neq 0$ et $D_1 \neq 0$ et  $D_2 \neq 0$ alors
      $\dfrac{N_1}{D_1} \times \dfrac{N_2}{D_2} = \dfrac{N_1N_2}{D_1D_2}$
    • Règle 11 :
      si $N_2 \neq 0$ et $D_1 \neq 0$ et  $D_2 \neq 0$ alors
      $\dfrac{\dfrac{N_1}{D_1}}{\dfrac{N_2}{D_2}} = \dfrac{N_1}{D_1} \times \dfrac{1}{\dfrac{N_2}{D_2}} = \dfrac{N_1}{D_1}\dfrac{D_2}{N_2} = \dfrac{N_1D_2}{N_2D_1}$
    • Règle 12 : Le produit des termes extrêmes est égale au  produit des termes moyens :
      si $ B \neq 0$ et $D \neq 0$  alors
      $\dfrac{A}{B} = \dfrac{C}{D} \iff A \ D = B \ C$
  • 3 Identités remarquables dans le corps des réels $(R,+,\times)$
    Ces 3 identités sont valables  dans tout anneau commutatif $(A,+,\times)$

    • IR1 : $\boxed{(a + b)^2 = a^2 + 2ab + b^2}$
      Le carré d'une somme est la somme du double produit et de la somme des carrés des deux nombres. 
      Le carré d'une somme n'est donc pas la somme des carrés.
      La fonction carré : $x \mapsto x^2$ n'est pas une fonction linéaire !!!
      Attention, il ne faut jamais oublier le double produit : vous pouvez le vérifier sur le schéma suivant :

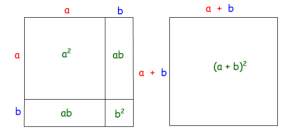      Démonstration :
      $(a +b)^2 = (a + b)(a + b) = aa +ab + ba + bb = a^2 + 2ab + b^2$ car $ab = ba$ à cause de la commutativité de la loi $\times$
    • IR2 : $\boxed{(a - b)^2 = a^2 - 2ab + b^2}$
      Démonstration :
      Cette IR2 obtient facilement à partir de la IR1 en remplaçant $b$ par $-b$.
      Attention, ici aussi il ne faut jamais oublier le double produit : vous pouvez le vérifier sur le schéma suivant :

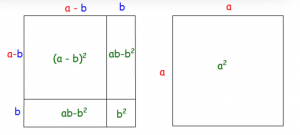
    • IR3  : $\boxed{(a + b)(a \ - \ b) = a^2 \ - \ b^2}$
      Démonstration :
      $(a + b)(a \ - \ b) = a^2 \ - \ ab  \ + \ ab  \ - \ b^2 = a^2 \ - \ b^2$
      On peut vérifier cette identité remarquable sur le graphique suivant :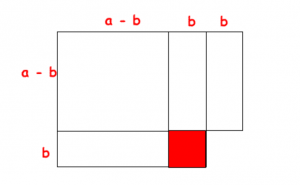
      Cette identité remarquable IR3 , la plus importante des trois est très utile Par exemple, en calcul mental.
      Exemple :
      $101 \times 99 = (100 + 1)(100 - \ 1) = 100^2 - \ 1^2 = 10000 - \ 1 = 9999$
    • Il y a bien sûr d'autres identités remarquables :
      $\boxed{(a + b + c)^2 =a^2 + b^2 + c^2 + 2ab + 2ac + 2bc}$
      $\boxed{a^3 + b^3 = (a + b)(a^2 \ - \ ab + b^2)}$
      $\boxed{a^3 \ - \ b^3 = (a \ - \ b)(a^2 + ab +b^2)}$
      $\boxed{\forall n \geq 2 \qquad a^n - b^n = (a \ - \ b)(a^{n \ - \ 1} + a^{n \ - \ 2}b + a^{n \ - \ 3}b^2 + \cdots + ab^{n - \ 2} + b^{n \ - \ 1}}$
    • On peut retrouver la formule du binôme de Newton dans un anneau commutatif ou avec des éléments $a$ et $b$ permutables dans un anneau c'est-à-dire tels que $ab = ba$
      $\boxed{\displaystyle{(a + b)^n = \sum_{k=1}^n \begin{pmatrix} n \\ k \end{pmatrix} \  a^k \ b^{n \ - \ k}}}$
      grâce au Triangle dit du français Blaise PASCAL  mais découvert dans les manuscrits antérieurs du  chinois SHI CHOU YIE et de l'indien BASKARA
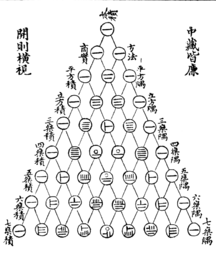
    • Attention !

      Dans un anneau où la multiplication n'est pas commutative ,par exemple l'anneau des matrices carrées d'ordre $n$, il existe des matrices $A$ et $B$ telles que $AB \neq BA$ alors
      $\boxed{(A + B)^2 = (A + B)(A + B) = AA + AB + BA + BB = A^2 + AB + BA + B^2}$
    • Exercices
      • Calculer mentalement 1012; 2042; 101 x 99 ; 394 x 406 ; 472- 432
      • Compléter les égalités suivantes :

        x2+ ..................... + 25 = ( ...... + .......)2
        x2-..................... + 16 = ( ...... - .......)2x2-..................... + 16 a2= ( ...... + .......)2x2- ..................... + 16 a2= ( ...... -.......)2x2+ 8 x + ........ = ( ...... + .......)2x2- 10 x .....................= ( ...... -.......)2

        x2+ 6 x + ......... = ( ...... + .......)2

        x2- 12 x ..................... + 16 = ( ...... -.......)2

        x2+ ..................... + b4= ( ...... + .......)2

        x2- ..................... + b4= ( ...... -.......)2

        a2b8+ ..................... + 64 = ( ...... + .......)2

        4x2y12- ..................... + 121 = ( ...... -.......)2