- Le nombre $\pi$
 Srinivasa RAMANUJAN (22/12/1887-26/04/1920 Inde)
Srinivasa RAMANUJAN (22/12/1887-26/04/1920 Inde)
L'un des plus grands mathématiciens mondiaux-
- $\int_{-\infty}^{+\infty} \frac{dt}{1 + t^2} \ dt = 2 \int_0^{+\infty} \frac{dt}{1 + t^2} \ dt = \pi$
-
- $ 2 \int_0^1 \frac{dt}{\sqrt{1 - t^2}} \ dt = \pi$
-
- $\int_a^b \frac{dt}{\sqrt{(t -a)(t -b)}} \ dt = \pi$
-
- Approximations décimales ou rationnelles de $\pi$ depuis l'Antiquité : Capes interne 1995
- Approximation par la méthode des isopérimètres
-
- Des lapins de Fibonacci (alias Leonard de Pise) au Nombre d'Or $\Phi$


- Sujet : Fibonacci
- Corrigé : fibonaccicorrige
- les 7 relations métriques d'un triangle rectangle et quelques relations métriques d'un triangle quelconque.
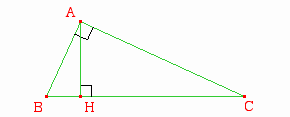
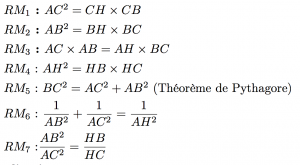
- Sujet : Relationsmetriques
- Corrigé :
- Autres relations métriques
- Thalès, Menelaus et Ceva
- Sujet : thalesmenelaus
- Corrigé :
- Puissance d'un point par rapport à un cercle
- Sujet :puissance
- Corrigé : puissanceptcor
- L'inversion
- Sujet : inversion
- Corrigé : inversionseul
- Irrationnalité de $\zeta(2)$
- Les fonctions eulériennes $\beta$ et $\Gamma$
- $Gamma$ et loi du $\chi_2$ :
- Sujet capes agricole 08 :capesagricole08c1
- Corrigé capes agricole 08 :capesagricole08e1scor
- $Gamma$ et loi du $\chi_2$ :
- Les fonctions trigonométriques et hyperboliques inverses :
- La fonction $\chi_2$
Aller au contenu

