Relations binaires

  • Propriétés d'une relation :
    Soit un ensemble $E$ muni d'une relation $\mathcal{R}$. On note $\Gamma$ l'ensemble des couples $(x,y)$ tels que $x \ \mathcal{R} \ y$.
    Cet ensemble $\Gamma$ s'appelle le graphe de la relation $\mathcal{R}$.
    $\Gamma \subset E \times E$.

    • Une relation $\mathcal{R}$ est réflexive lorsque $\forall x \in E \qquad x  \ \mathcal{R} \ x$
    • Une relation $\mathcal{R}$ est symétrique lorsque $\forall x \in E \quad \forall y \in E \qquad x  \ \mathcal{R} \ y \Longrightarrow y \ \mathcal{R} \ x$
    • Une relation $\mathcal{R}$ est antisymétrique lorsque $\forall x \in E \quad \forall y \in E \qquad x  \ \mathcal{R} \ y \text{ et } y \ \mathcal{R} \ x \Longrightarrow x = y$
    • Une relation $\mathcal{R}$ est transitive lorsque $\forall x \in E \quad \forall y \in E \quad \forall z \in E \qquad x  \ \mathcal{R} \ y \text{ et } y \ \mathcal{R} \ z \Longrightarrow x \ \mathcal{R} \ z$
  • Relation d'équivalence :
    • Une relation $\mathcal{R}$ est dite relation d'équivalence lorsqu'elle est réflexive, symétrique et transitive.
    • $Cl(x) =\{ y \in E / x \ \mathcal{R} \ x \}$ s'appelle la classe d'équivalence de $x$ et se note par exemple $\bar{x}$ ou $\dot{x}$.
      C'est une partie de l'ensemble $E$ donc un élément de $\mathcal{P}(E)$.
    • L'ensemble des classes d'équivalence de $E$ pour la relation d'équivalence $\mathcal{R}$ s'appelle l'ensemble-quotient de $E$ par $\mathcal{R}$ et est noté $E/\mathcal{R}$
    • Les éléments de $E/\mathcal{R}$ en tant que parties de $E$ constitue une partition de $E$.
    • L'application 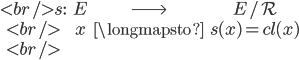 est surjective. Elle est appelée surjection canonique.
      Alors $x \ \mathcal{R} \ y \iff s(x) =s(y)$
    • Si $f$ est une application de $E$ dans $F$ alors
      On peut définir une relation d'équivalence $\mathcal{R}$ dans $E$ par $x \ \mathcal{R} \ y \iff f(x) = f(y)$.
      De plus l'application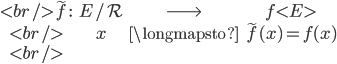  est bijective.
      L' application $f$ va se factoriser en $f = i \ \circ \ \widetilde{f} \ \circ \ s$
      où $i$ est l'injection canonique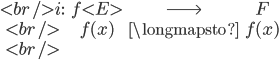  
    • Exemples de relation d'équivalence :
      • Dans $Z \times Z^*$ la relation $(a,b)  \ \mathcal{R} \ (c,d) \iff ad = bc$ est une relation d'équivalence.
        L'ensemble $Z \times Z^* /\mathcal{R}$ est $Q$ l'ensemble des nombres rationnels.
  • Relation d'ordre :
    • Une relatiosn $\mathcal{R}$ est dite relation d'ordre si elle est réflexive, antisymétrique et transitive.
      Cet ordre et dit total si $\forall x \in E \quad \forall y \in E \qquad x \mathcal{R} y \text{ ou } y \mathcal{R} x$.
      Si $\exists x \in E \quad \exists y \in E $ tels que l'on n'a pas $x \mathcal{R} y $ et l'on n'a pas $y \mathcal{R} x$ cet ordre est dit partiel.
    • Exemples :
      • $\leq$ est une relation d'ordre total dans $R$.
      • la relation de divisibilté $\mid$ dans $Z$ est une relation d'ordre partiel car par exemple $2$ ne divise pas $3$ et $3$ ne divise pas $2$.
  •  Exercices
    • Ex 1  : On définit dans une population $P$ finie la relation suivante "a un ami".
      On sait que cette relation $\mathcal{R}$ est antiréflexive(c'est-à-dire que personne n'est son propre ami) et symétrique.
      On sait de plus qu'il y a au moins une personne qui a un ami et que si $2$ personnes ont le même nombre d'amis, ils n'ont pas d'amis communs.
      Démontrer qu'il y a au moins une personne qui n'a qu'un seul ami.