Les ensembles de nombres

  • Cours personnel sur les Ensembles :

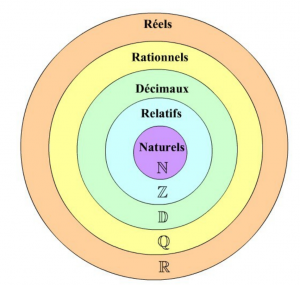
    ch03ec1
  • Les Ensembles de nombres :
    • vidéo des Amphis de la 5 (Professeur Jacques VAUTHIER) sur la construction des nombres réels :
      https://youtu.be/oKeMGn6-GQE?t=182
    • vidéo des Amphis de la 5 (Professeur Jacques VAUTHIER) sur l'ensemble Q des nombres rationnels et l'ensemble R - Q des nombres irrationnels :
      https://youtu.be/9fwRICvwmag?t=719
    • Quelques résultats classiques sur les irrationnels :

      • $\sqrt{2}$ est un irrationnel (Résultat connu depuis l'Antiquité)
        Lemme 1 : si $n$ est un entier pair alors $n^2$ est pair
        Ce lemme est équivalent à la contraposée : Si $n^2$ est impair alors $n$ est impair.
        Lemme 2 : Si $n$ est un entier impair alors $n^2$ est impair .
        Ce lemme est équivalent à la contraposée : Si $n^2$ est pair alors $n$ est pair
        Lemme 3 : On peut déduire des lemmes 1 et 2 les équivalences suivantes :
        - $n$ est pair $\iff n^2$ est pair.
        - $n$ est impair $\iff n^2$ est impair.
        Théorème : $\sqrt{2} \notin Q$.
        Démonstration par l'absurde :
        Supposons que $\sqrt{2} \in Q$ donc $\sqrt{2} =\dfrac{p}{q}$ où $p$ et $q$ sont premiers entre eux c'est-à-dire que la fraction $\dfrac{p}{q}$ est irréductible.
        Donc $2 =\dfrac{p^2}{q^2}$ d'où $p^2 =2q^2$ donc $p^2$ pair donc $p$ pair donc $p=2p'$.
        Alors $(2p')^2 =2q^2$ d'où$q^2 =2p'^2$ donc $q^2$ pair d'où $q$ pair donc $q=2q'$.
        Mais alors $\sqrt{2} =\dfrac{p}{q} =\dfrac{p'}{q'}$ est réductible. Contradiction
    • Si $p$ est un entier premier alors $\sqrt{p}$ est un irrationnel
    • Corollaire : $\sqrt{2},\sqrt{3},\sqrt{5},\cdots$ sont des irrationnels
  • Les nombres algébriques et les nombres transcendants :
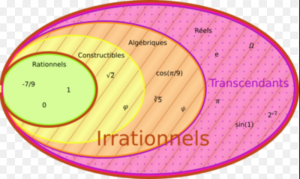
    Travail de recherche en cours...
  • Problèmes sur les irrationnels :
    • Capes Externe 2013 épreuve 1 : (Partie A : Exemples de nombres irrationnels - Partie B : Une preuve de l'irrationalité de $\pi$)