- Cours personnel sur les séries : disponible bientôt
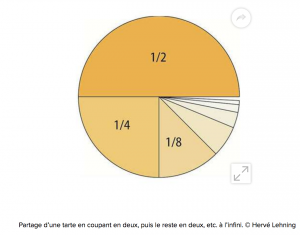
- Problèmes classiques :
- la série harmonique divergente $\zeta_1$ = $\displaystyle{\sum_{k = 0}^{+\infty} \dfrac{1}{n}}$
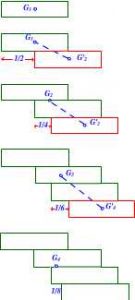
L'évêque Nicole d'Oresme(1325-1382) maître d'oeuvre de construction d'églises a étudié les empilements de briques sans mortier réalisés par les maçons de l'époque. il a compris que pour garder la structure d'une voûte en équilibre , il faut que le centre de gravité de la brique supérieure soit encore au dessus de la brique inférieure :
Si l'on veut placer par exemple 2 briques sur une 3ème, le centre de gravité commun $G_2$ des deux précédentes se trouve au bord de la 3ème donc du bord droit de la brique 1 à
$\dfrac{(1 \times \dfrac{1}{2} + 1 \times 1)}{2} = \dfrac{3}{4}$ d'unité.
La brique 4 est à placer au centre de gravité $G_3$ des 3 supérieures, c'est-à-dire avec un décalage de
$\dfrac{(2 \times \dfrac{3}{4} + 1 \times \dfrac{5}{4})}{2} = \dfrac{11}{12}$ brique.
Les décalages successifs sont $\dfrac{1}{2} + \dfrac{1}{4} +\dfrac{1}{6} +\dfrac{1}{8} + \cdots =
2( \dfrac{1}{1} + \dfrac{1}{2} + \dfrac{1}{3} +\dfrac{1}{4} +\dfrac{1}{5} + \cdots ) $
Nicole d'Oresme a démontré que la série harmonique est divergente
(Source : extrait du livre La Physique de tous les jours- Istvan Berkes - Editions Vuibert)
Ce problème d'empilement est très bien expliqué sur le site suivant :
http://prof.pantaloni.free.fr/IMG/pdf/Surplomb-de-briques.pdf - Cours personnel plus exercices : serieharmonique
- la série convergente $\zeta_2$ = $\displaystyle{\sum_{k = 0}^{+\infty} \dfrac{1}{n^2} = \dfrac{\pi^2}{6}}$ : PbDzeta2
- la série harmonique divergente $\zeta_1$ = $\displaystyle{\sum_{k = 0}^{+\infty} \dfrac{1}{n}}$
- Vidéo des Amphis de la 5 (Professeur Jacques VAUTHIER) sur les séries :
https://youtu.be/fuh5sEIfLn8?t=96
Aller au contenu

