Triangles

  • Inégalité triangulaire (La ligne droite est le plus court chemin):
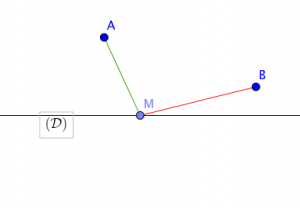
  • Les points importants :
    • Le centre de gravité  ou l'isobarycentre $G$ des points $A,B,C$ est le seul point vérifiant l'égalité vectorielle suivante :
      $\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0}$
      En notant $A'$ le milieu de $[BC]$ ,alors on a $\overrightarrow{A'B}  + \overrightarrow{A'C} = \overrightarrow{0}$ donc :
      $\overrightarrow{GA'} +  \overrightarrow{A'A} +\overrightarrow{GA'} + \overrightarrow{A'B} + \overrightarrow{GA'} + \overrightarrow{A'C} = \overrightarrow{0}$ d'où
      $3 \overrightarrow{GA'} + \overrightarrow{A'A'} = \overrightarrow{0}$
      $\overrightarrow{GA'} = \dfrac{1}{3} \overrightarrow{AA'}$.

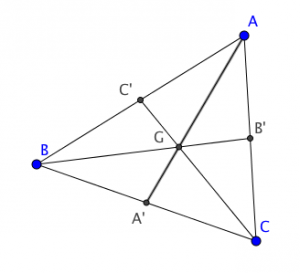
      Par conséquent, le centre de gravité $G$ est le point de concours des 3 médianes $(AA'),(BB'),(CC')$.
      Il est situé sur chaque médiane au $\dfrac{1}{3}$ de la base et à $\dfrac{2}{3}$ du sommet.
    • L'orthocentre $H$ st le point de concours des hauteurs.
    • Le centre du cercle circonscrit $O$ est le point de concours des médiatrices.
    • Le centre du cercle inscrit $I$ est le sprint de concours des bissectrices intérieures.
    • $O,G$ et $H$ sont alignés sur une droite dite Droite d'EULER avec la relation suivante
      $\overrightarrow{OH} = 3 \overrightarrow{OG}$
      Pour maîtriser ce thème , je vous propose un sujet sur la Droite d'Euler: Euler
  • Thalès et sa réciproque :
    • Thalès Triangle et Thalès Papillon:
      Soit un triangle $ABC$.

      - Si $M$ est un point de la droite $(AB)$ différent de $A$
      - Si $N$ est un point de la droite $(AC)$ différent de $A$
      - Si $(MN)$ et $(BC)$ sont parallèles
      Alors $\dfrac{AM}{AB} = \dfrac{AN}{AC} = \dfrac{MN}{BC} $
    • Corollaire : Théorème 1 des milieux
      La droite qui passe par le milieu d'un  côté d'un triangle et qui est parallèle à un autre côté passe alors par le milieu du troisième côté.
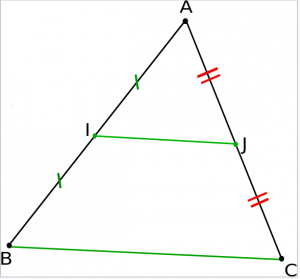
    • Réciproque Thalès triangle :
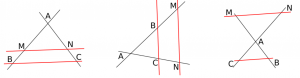
      Dans le cas d'une des trois figures suivantes :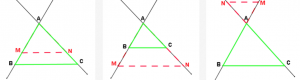
      Si l'on a $\dfrac{AM}{AB} = \dfrac{AN}{AC}$  alors les droites $(MN)$ et $(BC)$ sont parallèles. 
    • Corollaire : Théorème 2 des milieux
      La droite qui joint les milieux de deux côtés d'un triangle est parallèle au troisième côté.
  • Pythagore et sa réciproque  :

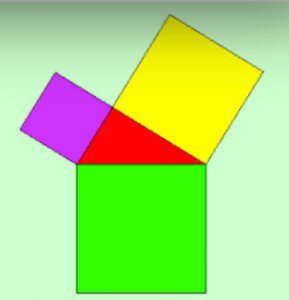
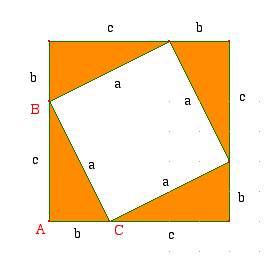
    • Si un triangle $ABC$ est rectangle en $A$ alors $BC^2 = AB^2 + AC^2$
    • Si dans un triangle $ABC$ on a $BC^2 = AB^2 + AC^2$ alors $ABC$ est rectangle en $A$.
  • Relations métriques :

    • dans un triangle rectangle
    • dans un triangle quelconque
  • Triangle équilatéral
    "Je suis allé trop loin
    Avec mon souci d'ordre 
    Rien ne peut plus venir"
    GUILLEVIC - Comptines euclidiennes - Poésie - Gallimard 1967

    • Hauteur dans un triangle équilatéral
    • La somme des distances d'un point intérieur aux 3 côtés est constant et vaut la valeur de la hauteur.
  • Triangle rectangle
    • Théorème de Pythagore
    • Triangle inscrit dans un demi-cercle.